※この記事はUnity及びBlenderの素人が調べながら作業したときの記録です。ベストプラクティスではありませんのでご注意ください。
目次
はじめに
VRChat想定アバター、ティグリなすちゃん(以下、なすちゃん)をAvatar3.0にアップデートしました。
また、なすちゃんはポニーテールバージョンとピッグテールバージョンの2種類あります。
この2種類は別々のアバターのため、独自のExpressionを実装して1つのアバターで両方の髪型を変更にできるにしました。
そのときの作業の記録です。
この記事の内容
この記事で説明していること
- なすちゃんをAvatar2.0からAvatar3.0にアップデートする
- なすちゃんの髪型をExpressionsで変えられるようにする
この記事で説明していないこと
説明具合
読者はBlenderをあまり操作した経験がないことを想定しますので、Blenderでの操作については詳しく記載します。
Unityでの作業はある程度経験があることを想定します。Unityでの操作説明は多少端折ります。
(これは筆者の作業当初の状態です)
作業環境
使用したアセット
本記事では必要
必要ではない
工程
1. なすちゃんを購入
兎にも角にも、なすちゃんを購入しダウンロードします。これが無いと始まりません。
3000円と比較的安価で何よりも可愛いので皆さん購入しましょう。
2. なすちゃんの髪のパーツを分割する
以下の工程では、このページをもとにBlender内のウィンドウを呼称します。
blender-cg.net
また、UIは日本語とし、ショートカットはデフォルトのままとして説明します。
まずはBlenderで3Dモデルを開きます。
Tigri_Nasu.zip(なすちゃんのアーカイブファイル)を解凍して得られるフォルダ内にある「nasu_Pigtails_PC.fbx」及び「nasu_Ponytail_PC.fbx」の両方をインポートします。「nasu_Pigtails_PC.fbx」はピッグテールで「nasu_Ponytail_PC.fbx」はポニーテールのなすちゃんです。
fbxファイルのインポートは、ファイル > インポート > FBX(.fbx)で行います。
モデルを開くとアウトライナーは以下のようになります。Armature、Armature.001の左横の三角マーク(▶)を押せば階層が表示されます。
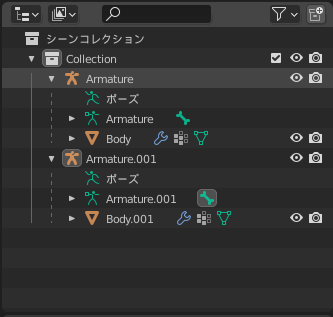 nasu_Pigtails_PC.fbxとnasu_Ponytail_PC.fbxをインポートしたときのアウトライナー
このArmatureはそれぞれのモデルファイルオブジェクトを表すものですが、このままの名前ではわかりにくいので以下のように名前を変更します。名前の変更は、オブジェクトにフォーカスを当てた状態でFn2キーを押下することでできます。
nasu_Pigtails_PC.fbxとnasu_Ponytail_PC.fbxをインポートしたときのアウトライナー
このArmatureはそれぞれのモデルファイルオブジェクトを表すものですが、このままの名前ではわかりにくいので以下のように名前を変更します。名前の変更は、オブジェクトにフォーカスを当てた状態でFn2キーを押下することでできます。
 オブジェクトの名前の変更
Pigtailと名のついているものはnasu_Pigtails_PC.fbxをインポートしたもの、Ponytailと名の付いてるものはnasu_Ponytail_PC.fbxをインポートしたものです。
オブジェクトの名前の変更
Pigtailと名のついているものはnasu_Pigtails_PC.fbxをインポートしたもの、Ponytailと名の付いてるものはnasu_Ponytail_PC.fbxをインポートしたものです。
以降、変更した名前で説明していきます。
3Dビューに2つのモデルが表示されている状態は邪魔なので、Pigtailを非表示にします。
非表示は、アウトライナーから非表示にしたいオブジェクトの横にある目のマークをクリックして目をつむった状態のマークにすることでできます。
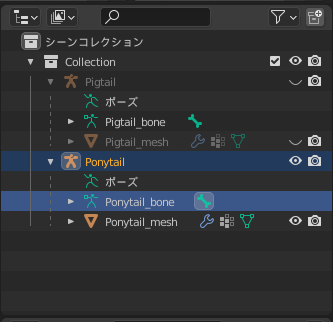 オブジェクトの非表示
オブジェクトの非表示
2.2. ポニーテールのメッシュを分離する
次に、ポニーテールのメッシュを分離します。
メッシュを分離するためには編集モードに移行する必要があります。
編集モードに移行するには、アウトライナーでメッシュ(Ponytail_mesh)を選択し、3Dビューの上にマウスカーソルを乗せてからTabキーを押下します。モデル上に線が網目状に表示されていれば編集モードに移行できています。
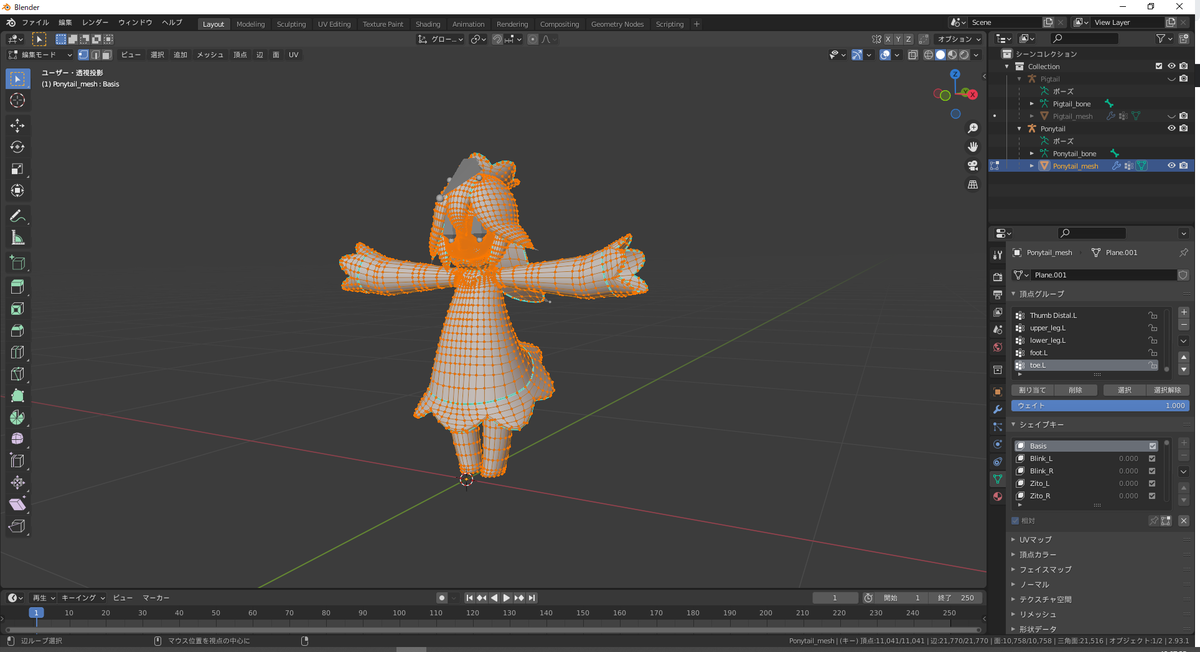 編集モードに移行した状態
ところで、編集モードに移行する前の状態は、デフォルトではオブジェクトモードと呼びます。モードによってできる操作が異なるため、操作がうまく行かない場合はモードを確認してください。
編集モードに移行した状態
ところで、編集モードに移行する前の状態は、デフォルトではオブジェクトモードと呼びます。モードによってできる操作が異なるため、操作がうまく行かない場合はモードを確認してください。
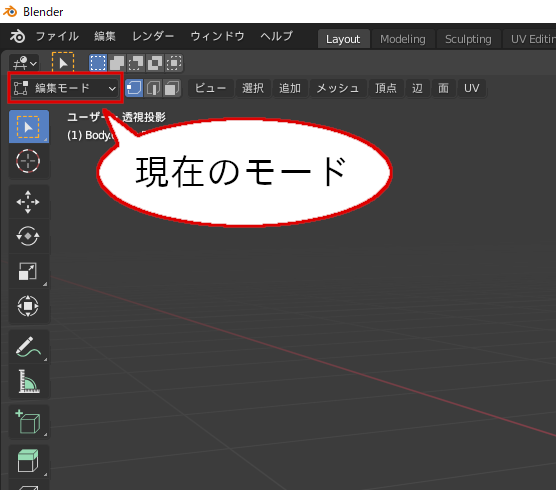 現在のモードを確認する
次に、ポニーテールの部分だけ分離するために、ポニーテールのメッシュのみを選択します。
現在のモードを確認する
次に、ポニーテールの部分だけ分離するために、ポニーテールのメッシュのみを選択します。
3Dビュー上でAlt+A*1を押下してメッシュの選択を解除します。その後、ポニーテールの上にマウスカーソルを乗せた状態でLキー*2を押下します。 これにより、ポニーテール全体が選択された状態になります。
ちなみに、3Dビュー上でモデルを拡大/縮小表示させるにはマウスホイールを回します。モデルを回転させるには、3Dビュー上の適当な場所でマウスホイールをドラッグします。
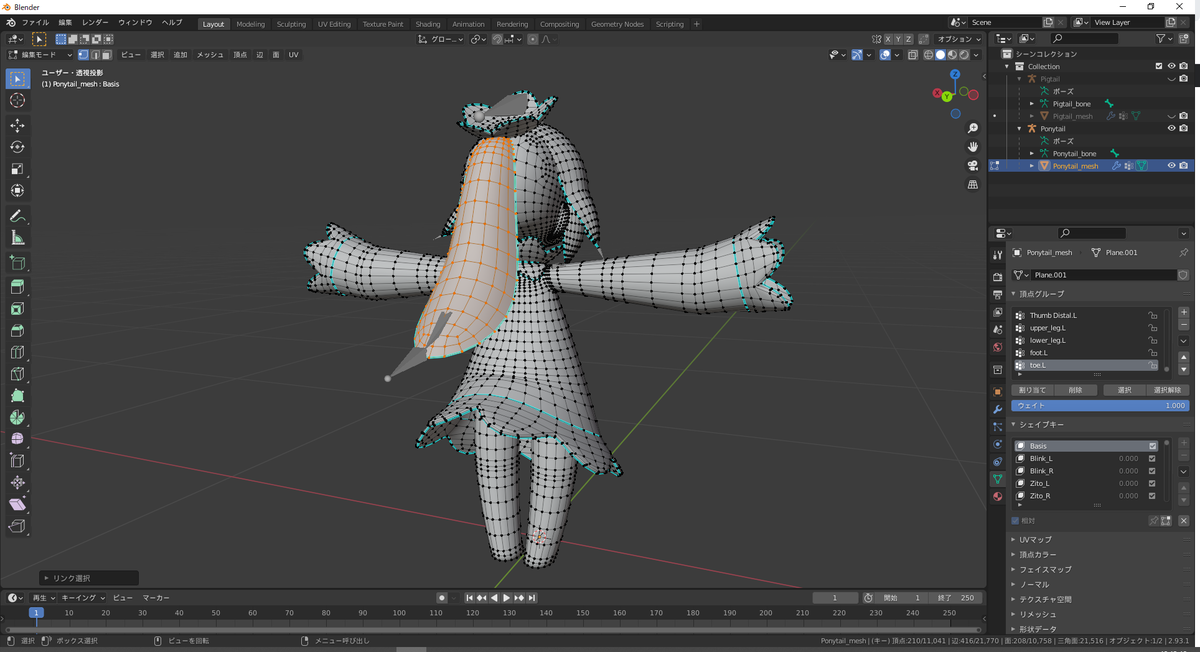 ポニーテール全体が選択されている状態
選択した後、3Dビューにマウスカーソルを乗せた状態でPキー*3を押し、表示された選択肢の「選択」をクリックすると、ポニーテール部分のメッシュを分離することができます。
ポニーテール部分のメッシュが分離された状態(左)、ポニーテール部分のメッシュ(Ponytail_mesh.001)が追加された(右)
分離が完了したら、Tabキーを押して編集モードを終了します。
ポニーテール全体が選択されている状態
選択した後、3Dビューにマウスカーソルを乗せた状態でPキー*3を押し、表示された選択肢の「選択」をクリックすると、ポニーテール部分のメッシュを分離することができます。
ポニーテール部分のメッシュが分離された状態(左)、ポニーテール部分のメッシュ(Ponytail_mesh.001)が追加された(右)
分離が完了したら、Tabキーを押して編集モードを終了します。
新たにできたメッシュの「Ponytail_mesh.001」は、「Ponytail_tail_mesh」と名前を変更します。
2.3. ポニーテールのボーンを分離する
続いて、ポニーテールのボーンを分離します。
アウトライナーでボーン(Ponytail_bone)を選択して、編集モードに移行します。ボーンの編集モードへの移行もTabキーでできます。
選択のやり方ですが、ボーンをクリックするとそのボーンを選択することができ、左クリックドラッグで範囲選択が可能です。あるボーンを選択したまま別のボーンも選択したい場合はShiftキーを押しながらクリックすることで選択できます。
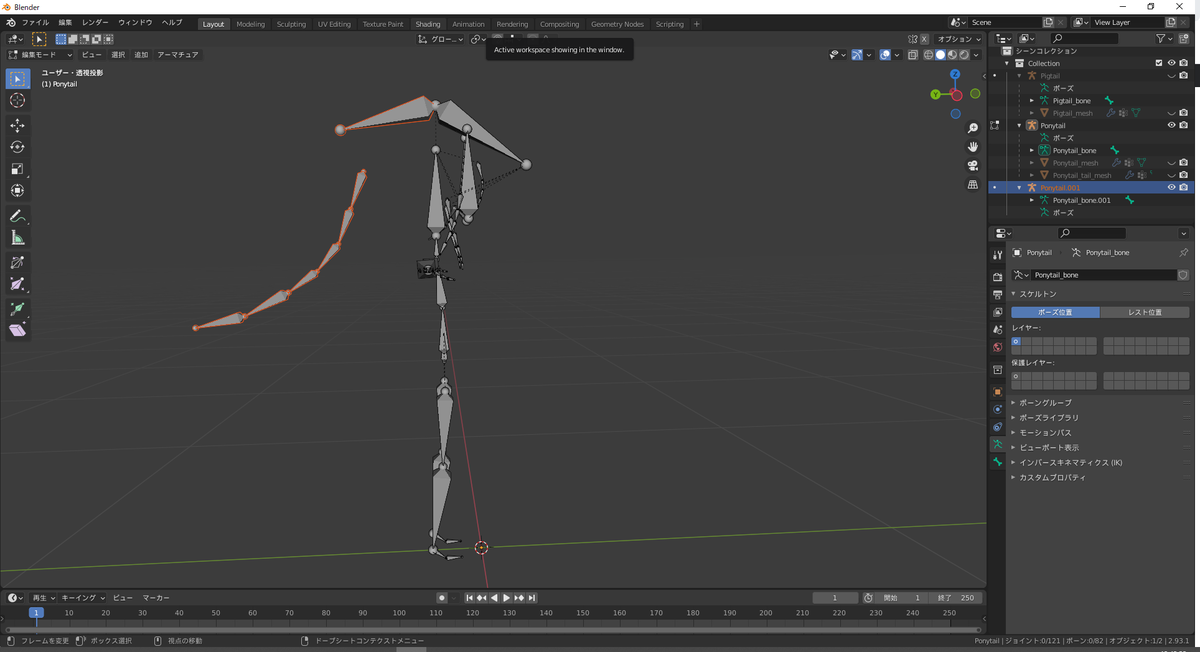
ここでは、ポニーテールに関わるすべてのボーンを選択します。ここでの選択すべきボーンは文字では説明しづらいので、画像を参考にしてください。なお画像はなすちゃんを横から見た状態であり、メッシュは非表示にしています。
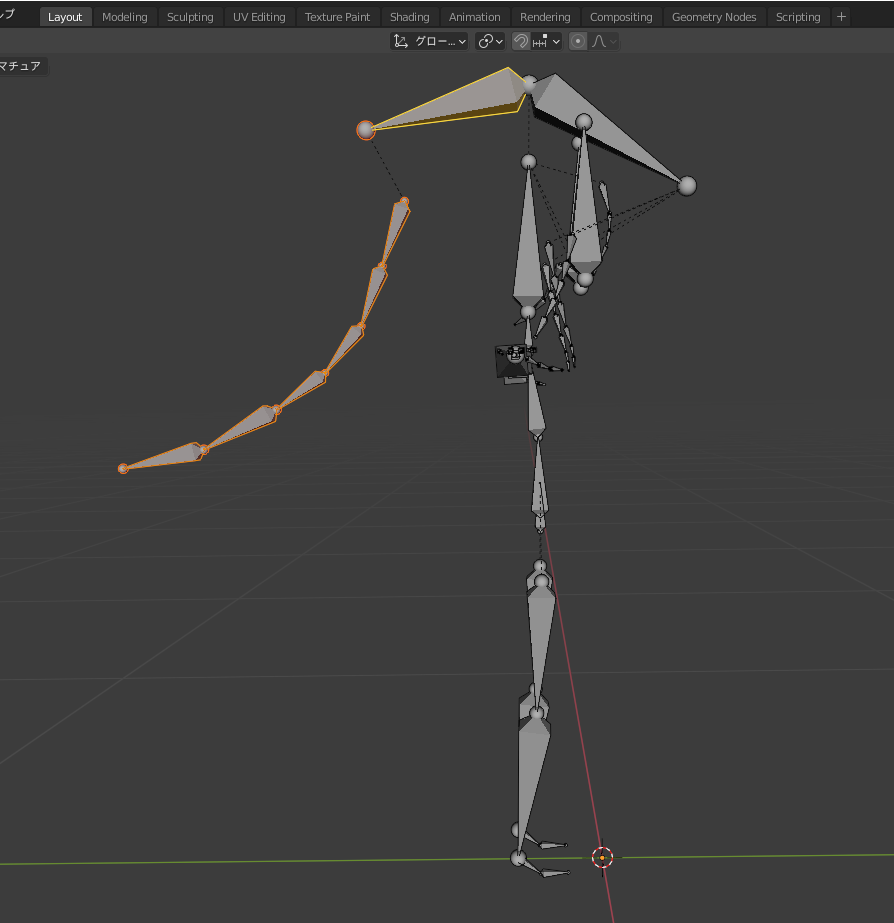 ポニーテールのボーンをすべて選択した状態
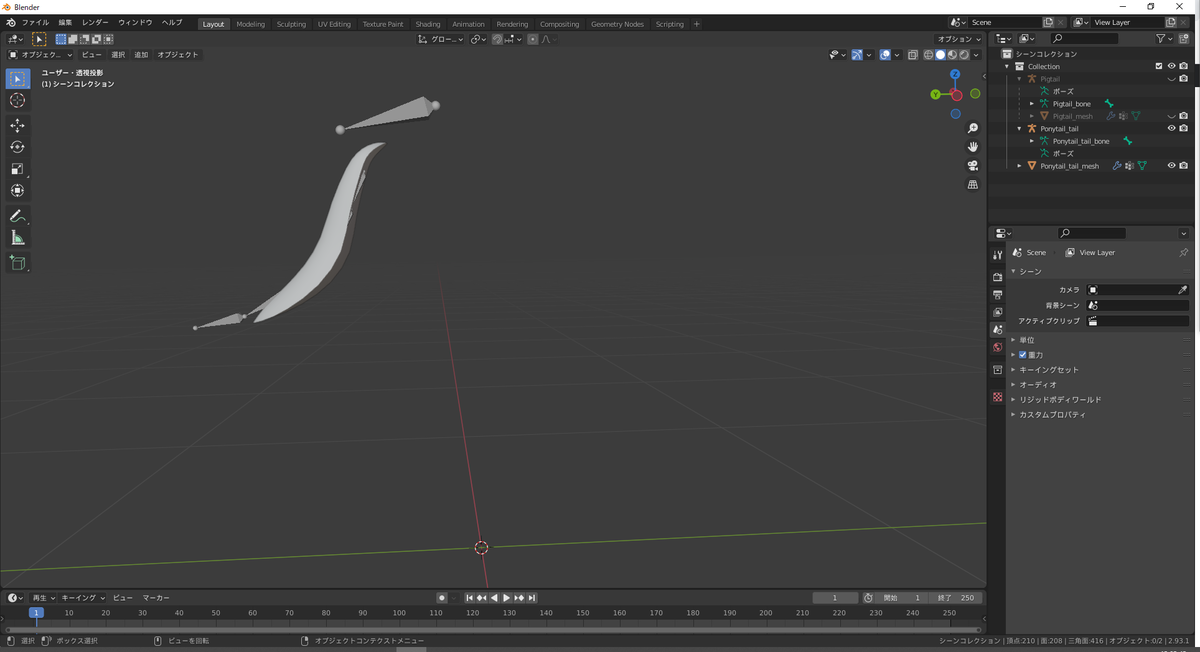
選択できたら、Pキーを押して「ボーンを別アーマチュアに分離」をクリックしてください。「Ponytail.001」というオブジェクトができたらOKです。
ポニーテールのボーンが分離された状態(左)と、ボーンのオブジェクト(Ponytail.001)が追加された状態
Ponytail.001という名前はわかりにくいので、「Ponytail_tail」と名前を変更し、階層の下にある「Ponytail_bone.001」は「Ponytail_tail_bone」と名前を変更しておきます。
ポニーテールのボーンをすべて選択した状態
選択できたら、Pキーを押して「ボーンを別アーマチュアに分離」をクリックしてください。「Ponytail.001」というオブジェクトができたらOKです。
ポニーテールのボーンが分離された状態(左)と、ボーンのオブジェクト(Ponytail.001)が追加された状態
Ponytail.001という名前はわかりにくいので、「Ponytail_tail」と名前を変更し、階層の下にある「Ponytail_bone.001」は「Ponytail_tail_bone」と名前を変更しておきます。
2.4. ポニーテールのメッシュとボーンを紐付ける
ポニーテールのメッシュとボーンはばらばらの状態になってしまったので、再度紐付けます。
編集モードになっている場合は、Tabキーを押下してオブジェクトモードに移行しておいてください。
最初に不要なオブジェクトを削除します。
Ponytailはポニーテールの部分以外は不要なので、ポニーテール以外のメッシュ及びボーンを削除します。
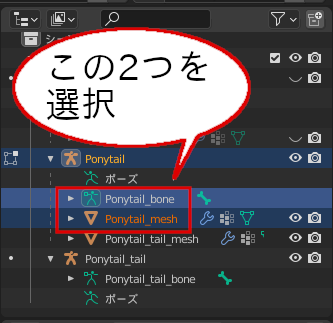
アウトライナーで「Ponytail_mesh」、「Ponytail_bone」を選択します。Xキーを押下することにより、選択したオブジェクトを削除できます。
不要なオブジェクトを選択(左)、オブジェクトを削除した状態(右)
次に、メッシュとボーンを紐付けていきます。
アウトライナーでPonytail_tail_mesh→Ponytail_tailの順に選択します。
選択した後、3Dビューにカーソルを乗せてからCtrl-P*4を押下し、選択肢の中から「自動のウェイトで」をクリックします*5。
そうすると、メッシュとボーンが同じオブジェクトの中に入ります。
 ポニーテールのメッシュとボーンを紐付けた
ここで、Ponytail_tail_boneの階層にある「Hair_B」というボーンの名前を「Pony_B」にしておきます。このボーンは後に使うためわかりやすい名前をつけておきます。
ポニーテールのメッシュとボーンを紐付けた
ここで、Ponytail_tail_boneの階層にある「Hair_B」というボーンの名前を「Pony_B」にしておきます。このボーンは後に使うためわかりやすい名前をつけておきます。
 Hair_BをPony_Bに変更
Hair_BをPony_Bに変更
2.5. ピッグテールのメッシュを分離する
次に、nasu_Pigtail_PCの方のピッグテールも分離します。
テールが2つあるので、片方のメッシュを選択した後にもう片方のメッシュも選択するようにします。そうすれば両方のテールが選択された状態になります。
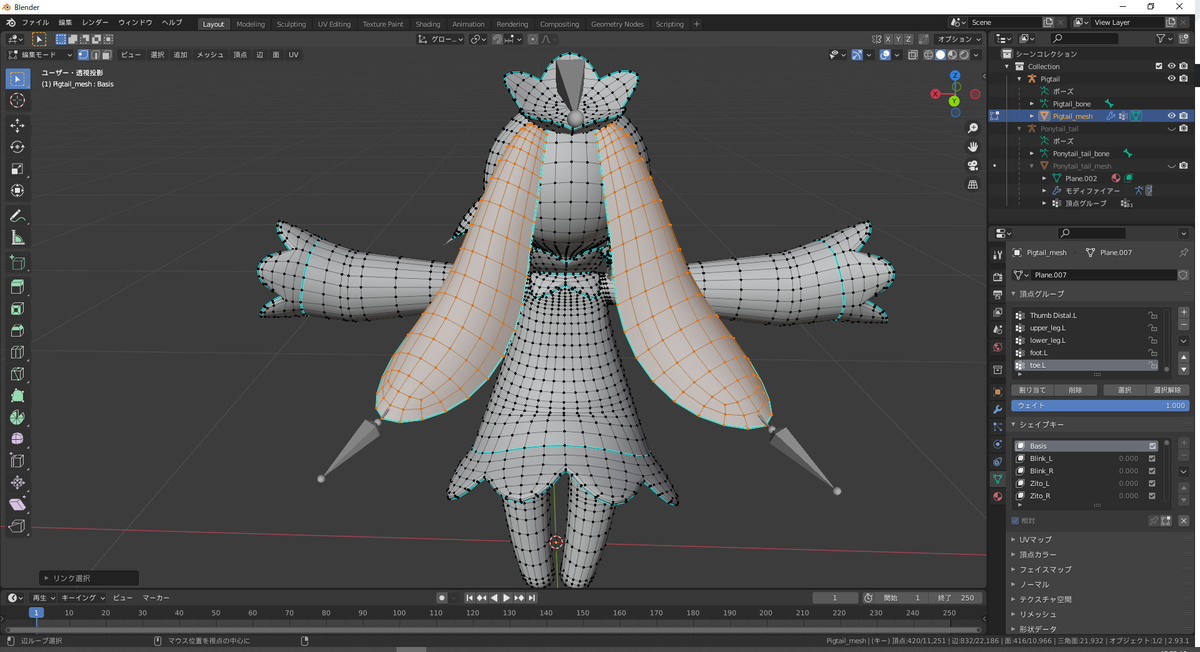 ピッグテールを選択した状態
選択したメッシュ分離します。分離したメッシュには「Pigtail_tail_mesh」と名付けます。
ピッグテールを選択した状態
選択したメッシュ分離します。分離したメッシュには「Pigtail_tail_mesh」と名付けます。
メッシュはボーンに紐付いたままなので、これ以上は操作しなくて大丈夫です。
2.6. ポニーテールを結合する
次に、Pigtailにポニーテールを結合させます。
作業前にオブジェクトモードに移行しておいてください。
アウトライナーで、Ponytail_tail→Pigtailの順に選択し、3Dビューにマウスカーソルを乗せてCtrl-J*6を押下します。
Pigtailの階層にPonytail_tail_meshが移動し、Pigtail_boneの階層にPony_Bが移動しているはずです。
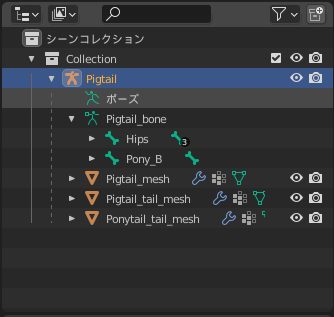 Pigtailの階層にすべてのオブジェクトが結合された
Pigtailの階層にすべてのオブジェクトが結合された
次に、ポニーテールのボーンを本体に接続します。
現在のポニーテールのボーンは本体とは離れていて、ポニーテールの部分が宙ぶらりんになっている状態です。そのため、本体とポニーテールを接続する作業が必要になります。
アウトライナーでPigtail_boneを選択して、編集モードに移行します。
ここで選択するべきボーンは近い位置にある(というより重なっている)ため、誤操作を避けるためにアウトライナーからボーンを選択するようにします。
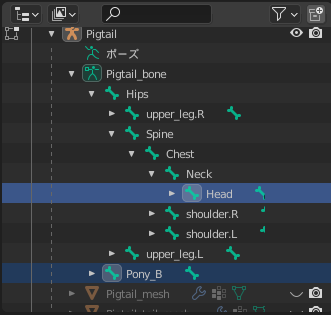
選択するべきボーンは2つで、「Pony_B」と「Head」です。Headの場所は「Hips > Spine > Chest > Neck > Head」と階層をたどった場所にあります。
「Pony_B → Head」の順番で選択してください。
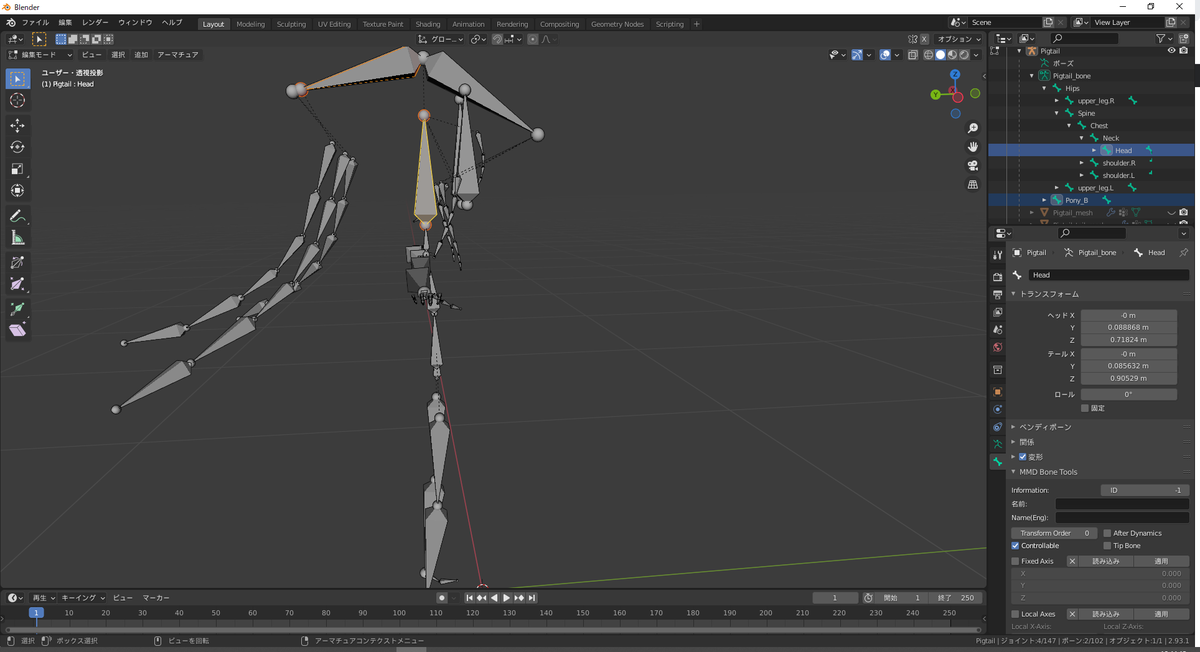
Pony_BとHeadを選択(左)、選択されたときの3Dビューの状態(右)
2つのボーンが選択できたら、3Dビューにカーソルを乗せてCtrl-Pを押下し、「オフセットを保持」をクリックします。Headの階層にPony_Bが移動していたらOKです。
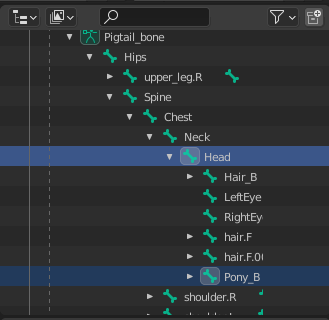 Headの階層にPony_Bが移動している
Headの階層にPony_Bが移動している
最後に、ポニーテールのメッシュとボーンを紐付けます。
オブジェクトモードに移行してください。アウトライナーでPonytail_tail_mesh→Pigtail_boneの順に選択します。その後、3Dビューにカーソルを乗せてCtrl-Pを押下し、「空のグループで」をクリックします。
これにより紐付けが完了しました。
2.7. メッシュとボーンが紐付いていることを確認する
メッシュとボーンが意図したとおりに紐付いているか確認します。
メッシュとボーンが紐付いてる状態とは、ボーンを動かすと連動してメッシュも動く状態です。
まずは、ポーズモードに移行します。ポーズモードとは、ボーンを動かすことができるモードです。
アウトライナーでPigtail_boneを選択し、Ctrl-Tabを押下してください。そうすることでポーズモードになります。
ボーンを選択すると、そのボーンが水色になります。
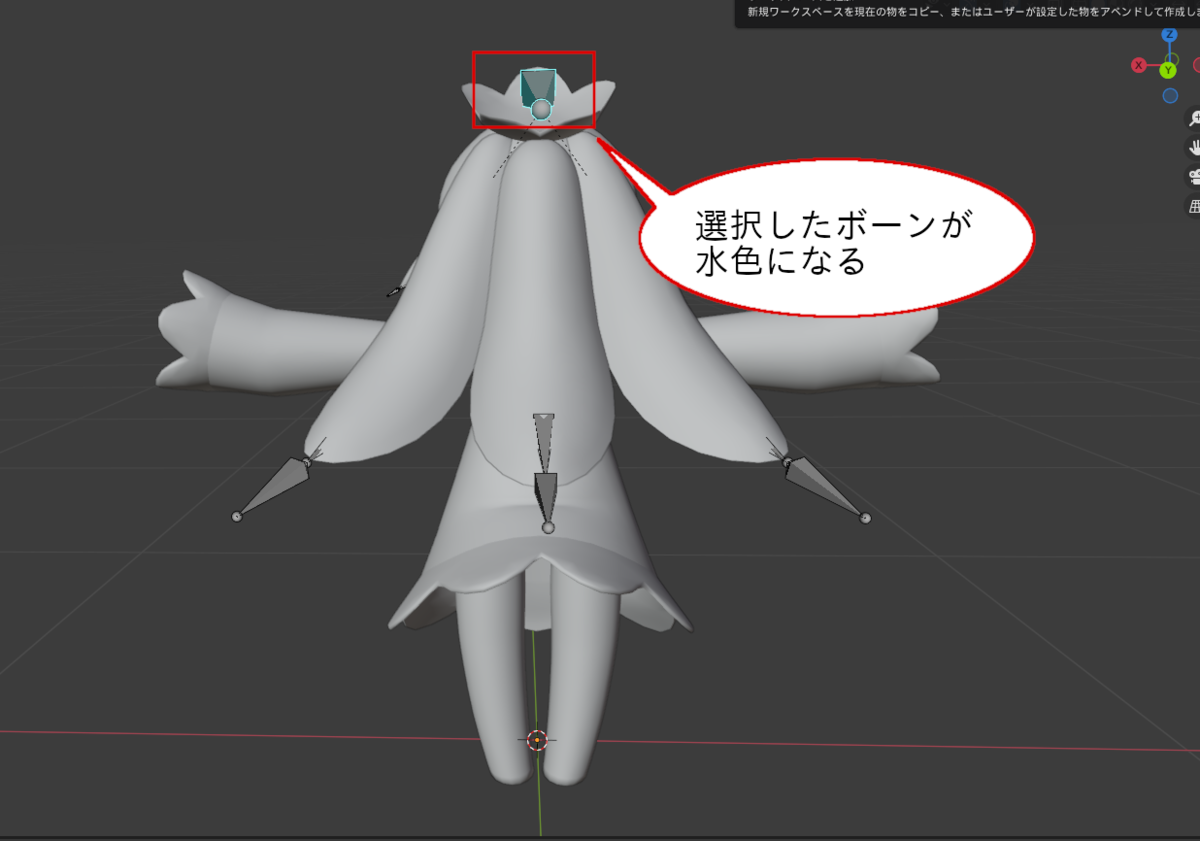 ポーズモードでボーンを選択した状態
ボーンを選択したらRキー*7を押下します。そうすれば、マウスでボーンを回転できるようになります。
ポーズモードでボーンを選択した状態
ボーンを選択したらRキー*7を押下します。そうすれば、マウスでボーンを回転できるようになります。
ポニーテールやピッグテールの根本のボーン(Hips > Spine > Chest > Neck > Head > Hair_BやPonyB)を選択して適当に動かしてみてください。髪の毛のメッシュも一緒に動けばメッシュとボーンが連動している状態です。
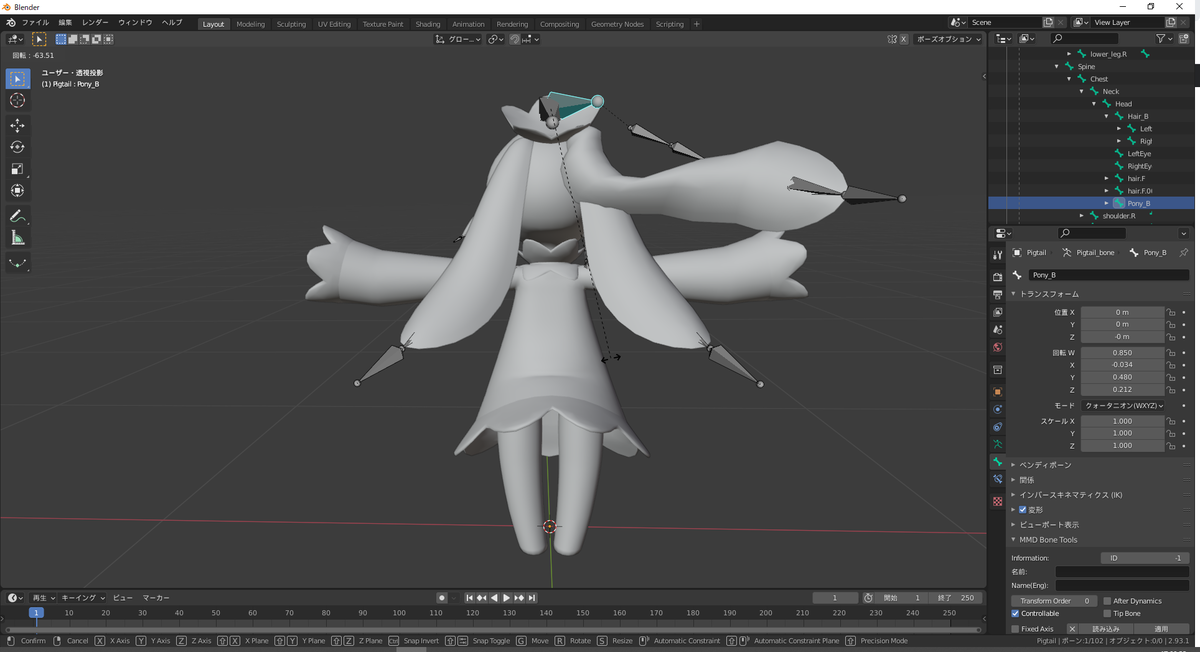 ポニーテールのボーン(Pony_B)を選択して動かした
左クリックでその位置にボーンを固定できます。また、クリックせずにEscキーを押下すればボーンを動かせる前の状態に戻ります。
ポニーテールのボーン(Pony_B)を選択して動かした
左クリックでその位置にボーンを固定できます。また、クリックせずにEscキーを押下すればボーンを動かせる前の状態に戻ります。
今回は初期状態のままにしておくので、クリックはせずにEscキーを押してください。クリックしてしまった場合はCtrl-Zを押して戻してください。
2.8. モデルをエクスポートする
作成したモデルをFBX形式でエクスポートします。
Unityでの整合性を合わせるために、エクスポートする前にオブジェクトの名前を変更します。
「Pigtail」を「Armature」、「Pigtail_mesh」を「Body」に変更してください。
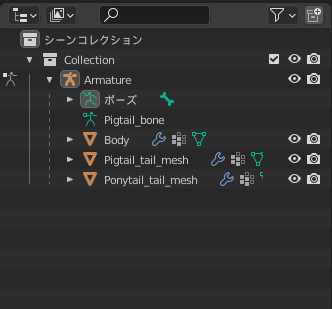 オブジェクトの名前を変更した
オブジェクトの名前を変更した
エクスポートは「ファイル > エクスポート > FBX(.fbx)」で行えます。適当な名前でFBXファイルを保存してください。本記事ではnew_nasu.fbxとします。
3. Avatar3.0に移行する
作業前にVRCSDK3.0-AVATARとユニティちゃんトゥーンシェーダー2.0、VRCAvatar3Toolsをダウンロードしておいてください。また、必要があればDynamic Boneを購入しておいてください。
3.1. Assetをインポートする
VRCSDK3.0-AVATAR、ユニティちゃんトゥーンシェーダー2.0、VRCAvatar3Tools、Dynamic Bone(必要であれば)、Tigri_Nasu、改変したなすちゃんのfbx(new_nasu.fbx)をインポートします。
それぞれ、Unitypackageファイルをダブルクリックすれば、現在開いているUnityプロジェクトにインポートできます。
メニューの Assets > Import Package > CustomPackage… からでもインポート可能です。
ここで、面倒を避けるためにTigri_nasuは他のUnitypackageを一通りインポートした後にインポートしてください。
Dynamic BoneはUnity Asset Storeで購入していれば、Package MangerからImportできます。
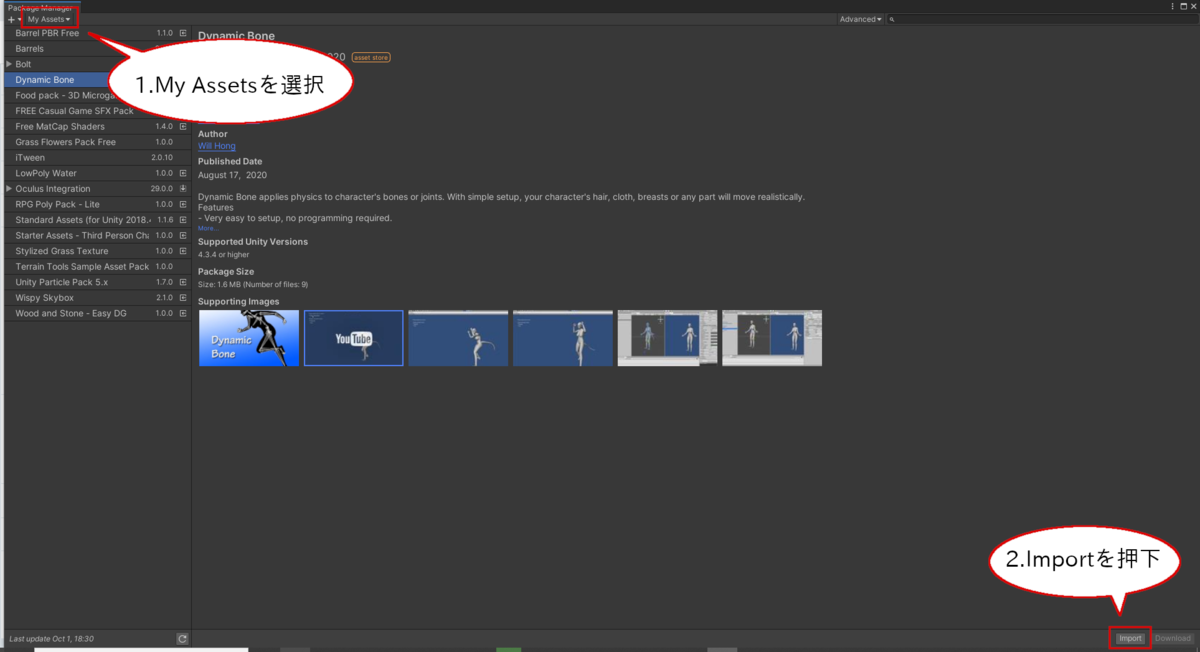 Package ManagerからDynamic Boneをインポートする
Package ManagerからDynamic Boneをインポートする
Tigri_Nasuをインポートした後、改変したfbxファイルをUnityプロジェクトにインポートします。
プロジェクトへのインポートは、エクスプローラーからファイルをプロジェクトにドラッグ&ドロップ(D&D)することでできます。
3.2. 改変したなすちゃんのモデルを設定する
改変したなすちゃんのモデルの設定を行います。
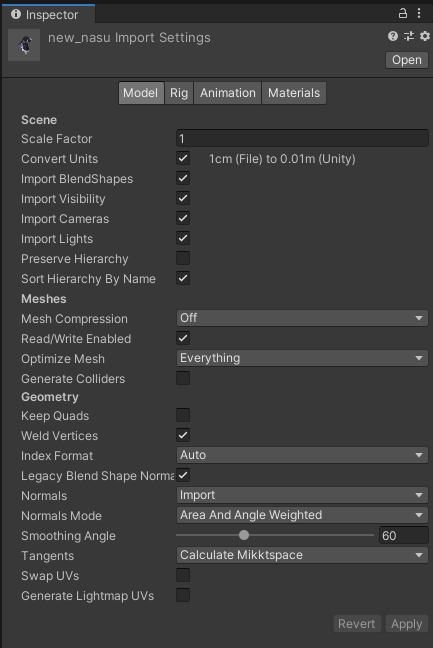
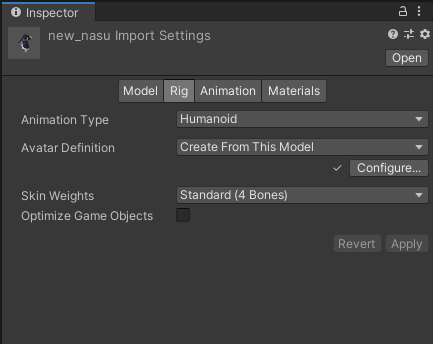
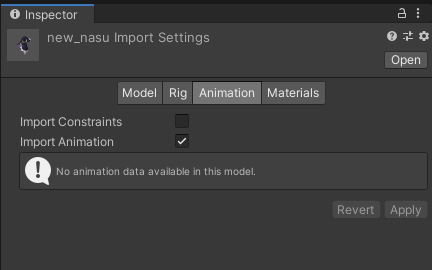
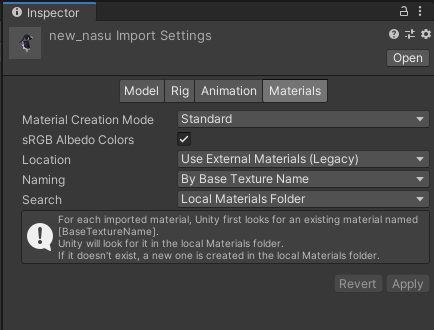
new_nasu.fbxを選択してInspectorでモデルの設定を行います。設定項目は「Model」、「Rig」、「Animation」、「Materials」の4つがありますが、それぞれ以下の画像のように設定してください。
new_nasu.fbxの設定
上記の設定の後、「Rig」タブを開いて「Configure…」からボーンの設定を行います。
「Mapping」タグから、「Body」、「Head」、「Left Hand」、「Right Hand」の4項目を設定できます。今回の場合は「Head」以外は特に設定をしなくて良いです。「Head」は以下の画像のように設定してください。
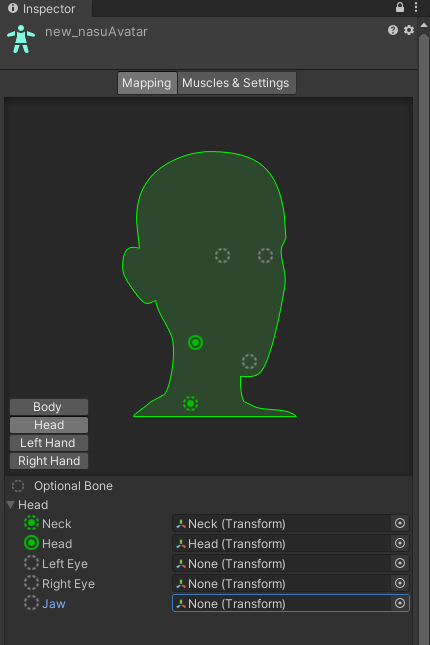 RigにおけるHeadの設定
RigにおけるHeadの設定
3.3. なすちゃんをAvatar3.0対応アバターにする
new_nasu.fbxのモデルをVRChat対応アバターにします。
まずは、Avatar3.0対応素体を生成します。
メニューからVRCAvatar3Tools > VRCAvatarConverterTo3を選択し、コンバーターを開いてください。
次に、「2.0 Avatar Prefab」の箇所で「nasu_Bou_PC」を選び、「Convert Avatar 3.0」をクリックします。
 nasu_Bou_PCをAvatar3.0にコンバート
Hierarchyにnasu_Bou_PC_3.0が生成されたと思います。
nasu_Bou_PCをAvatar3.0にコンバート
Hierarchyにnasu_Bou_PC_3.0が生成されたと思います。
コンバートした後は、nasu_Bou_PC_3.0に付いている「Missing」となっているコンポーネントを削除してください。
次に、new_nasuをHierarchyにD&Dし、Prefabをアンパックします。アンパックは、右クリックでコンテキストメニューを開き「Unpack Prefab Completely」をクリックで可能です。
nasu_Boud_PC_3.0の下にあるオブジェクトをすべて削除し、new_nasu配下にあるオブジェクトをすべて、nasu_Bou_PC_3.0の下に移動してください。
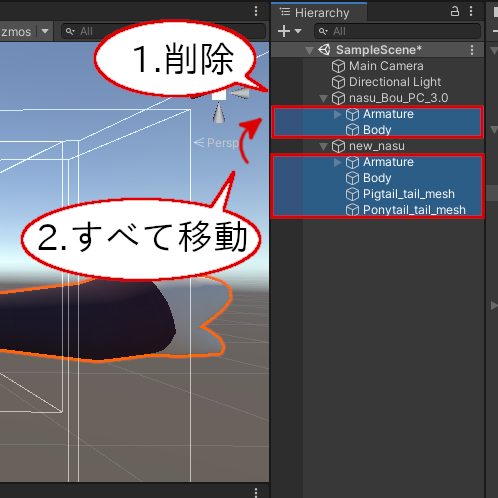 nasu_Bou_PC_3.0のオブジェクトを削除して、new_nasuのオブジェクトを移動する
移動した後はnew_nasuは削除して構いません。
nasu_Bou_PC_3.0のオブジェクトを削除して、new_nasuのオブジェクトを移動する
移動した後はnew_nasuは削除して構いません。
説明を簡単にするために「nasu_Bou_PC_3.0」は「nasu」と名前を変えておきます。
次に、LipSyncの設定を行います。
現状では、「VRC Avatar Descriptor (Script)」コンポーネントの「LikpSync」の項目が不正になっているので、これを変更します。
「Face Mesh」にnasuの下にあるBodyをD&Dしてください。
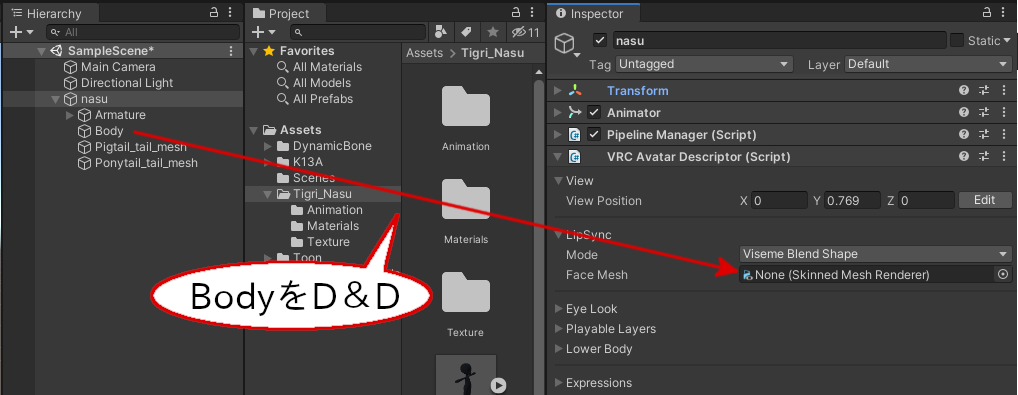 FaceMeshにBodyを設定
FaceMeshにBodyを設定
これで、VRChat用アバターとしての最低限の設定は完了しました。
3.4. 髪型を変更するExpressionsを作成する
Expressionsで髪型を変更できるようにします。
まずは、Assetsの適当な場所(Tigri_Nasuの下にフォルダを作ると良いでしょう)で、「Expressions Menu」、「Expressions Parameters」を新規に作成します。これらは、コンテキストメニューのCreate > VRChat > Avatarsから作成できます。それぞれ、「NasuMenu」、「NasuParams」と名前をつけておきます。
これらをnasuに紐付けます。nasuの「VRC Avatar Descriptor (Script)」の「Expressions」に、「Menu」と「Parameters」を設定する項目がありますので、それぞれに「NasuMenu」、「NasuParams」を設定してください。
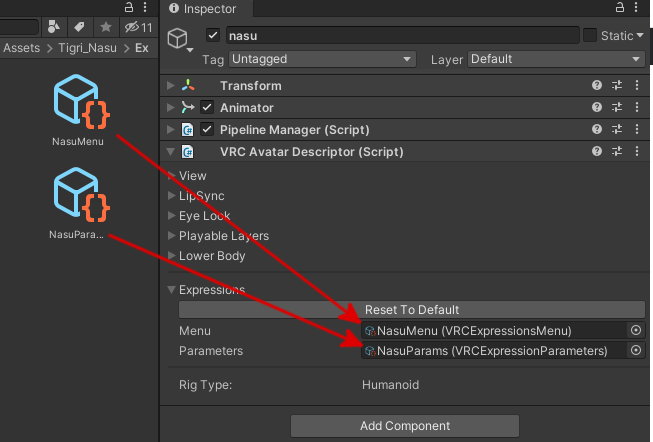 VRC Avatar DescriptorのExpressionsにMenuとParametersを設定
VRC Avatar DescriptorのExpressionsにMenuとParametersを設定
続いて、NasuParamsのパラメータを1つ増やします。
Inspectorの「Add」をクリックし、新しく生成された行を以下の画像のように設定します。
 NasuParamsにパラメータを追加
NasuParamsにパラメータを追加
パラメータを増やしたら、NasuMenuに髪型を変えるメニューを追加します。Inspectorの「Add Control」をクリックすることで、メニューが追加できます。以下の画像のように設定してください。
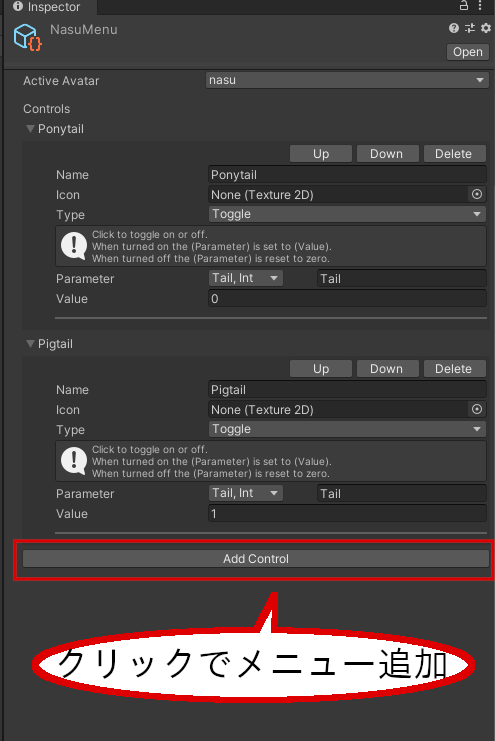 NasuMenuにメニューを追加
NasuMenuにメニューを追加
次に、アニメーションを作成します。
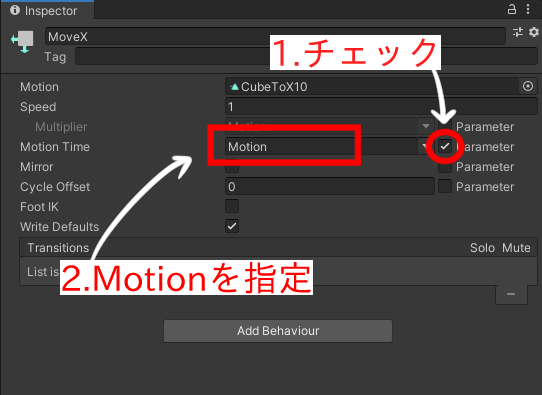
「Pigtail」というアニメーションを作成し、NasuにD&Dします。Animationウィンドウから、以下の画像のように設定します。
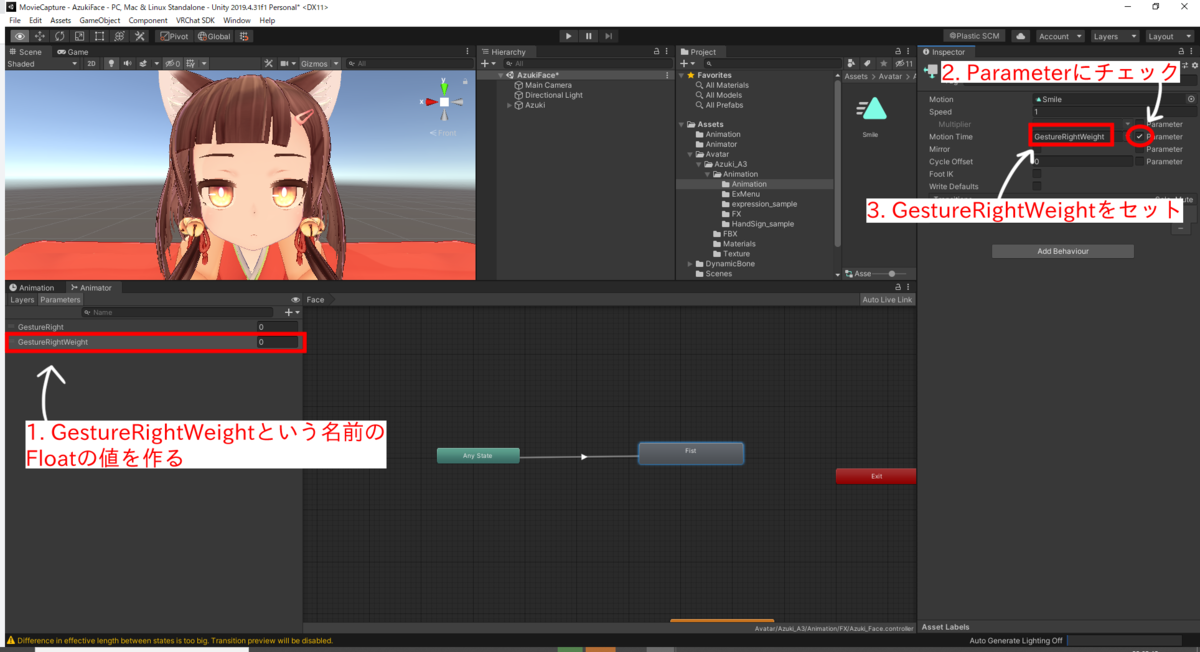
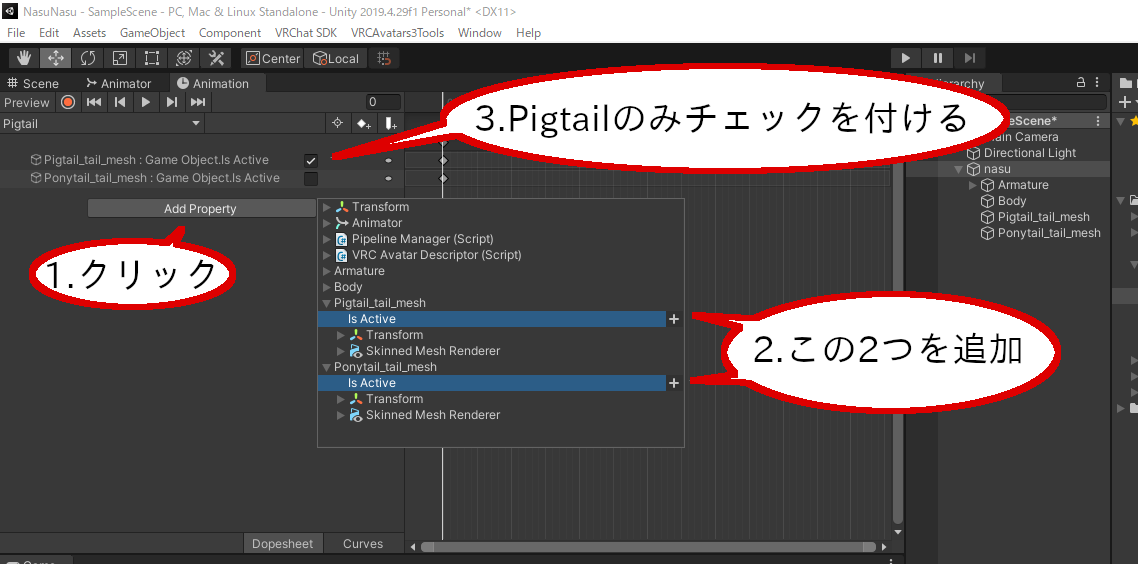 Pigtailアニメーションの設定
設定し終わったら、Pigtailアニメーションをコピーして、「Ponytail」という名前に変更します。
Pigtailアニメーションの設定
設定し終わったら、Pigtailアニメーションをコピーして、「Ponytail」という名前に変更します。
Ponytailのアニメーションは、Pigtailとは逆に、PonytailのIsActiveのみチェックを付けます。
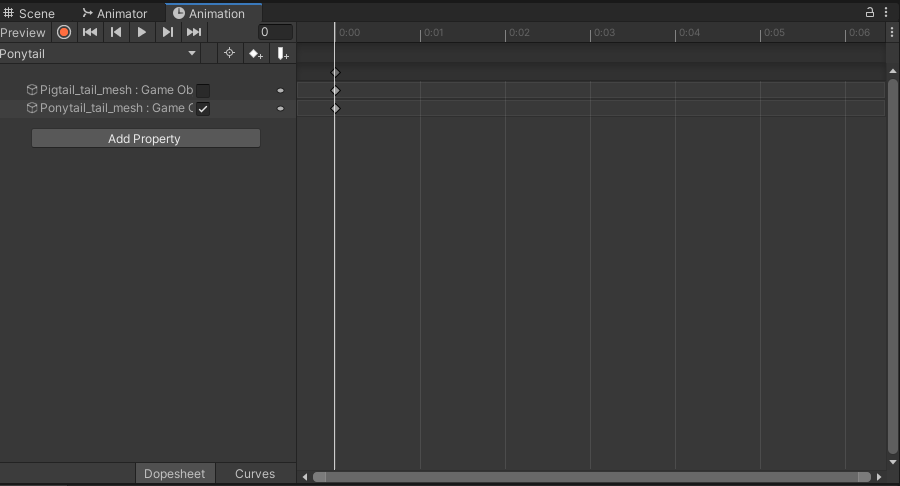 Ponytailアニメーションの設定
Ponytailアニメーションの設定
続いて、Animation Controllerの設定を行います。
AssetsのTigri_Nasu > Animationの下に「vrc_AvatarV3HandsLayer_nasu_Bou_PC 1」というAnimation Controllerができていると思います。これを編集していきます。
見つからない場合は、nasuのVRC Avatar Descriptorコンポーネントの「Playable Layers」にある「FX」に設定されているオブジェクトをクリックしてください。
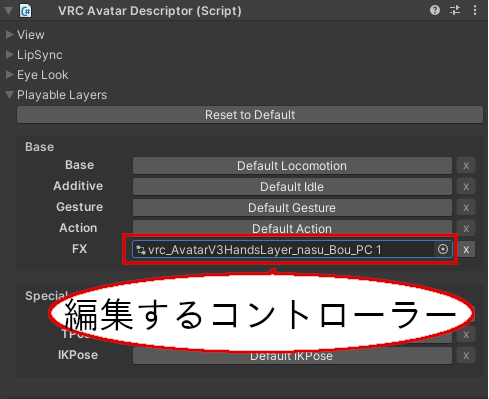 編集するべきAnimation Controller
Animatorウィンドウの、Layersタブでレイヤーを追加します。追加したレイヤーはTailと名付けます。
編集するべきAnimation Controller
Animatorウィンドウの、Layersタブでレイヤーを追加します。追加したレイヤーはTailと名付けます。
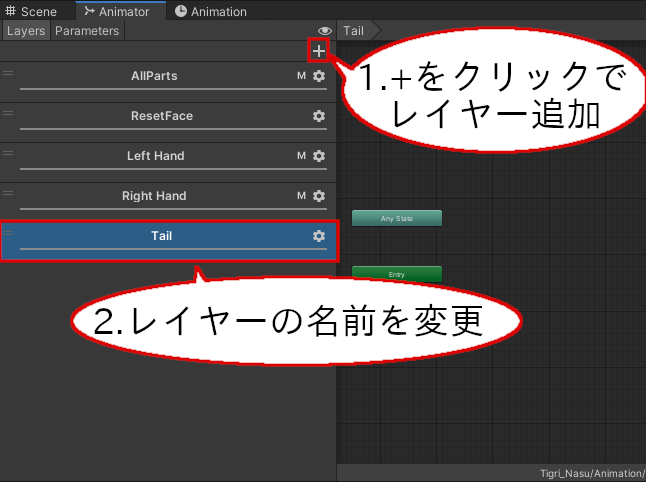 Animationレイヤー追加
追加したレイヤーの歯車マークを押して、Weightを1に設定します。
Animationレイヤー追加
追加したレイヤーの歯車マークを押して、Weightを1に設定します。
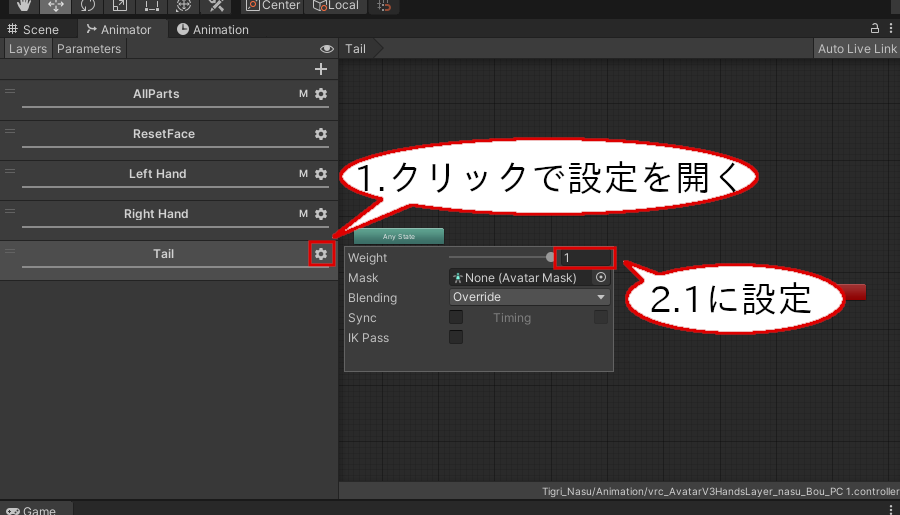 AnimationレイヤーのWeightを1にする
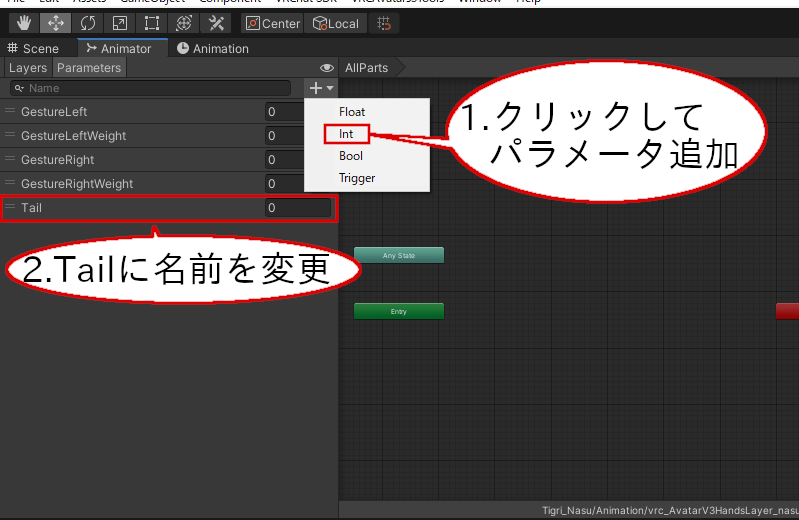
次に、Parametersタブでパラメータを追加します。追加するパラメータはIntで、名前をTailにします。
AnimationレイヤーのWeightを1にする
次に、Parametersタブでパラメータを追加します。追加するパラメータはIntで、名前をTailにします。
 Animationパラメータの追加
Animatorウィンドウに先ほど作成したPigtailアニメーションとPonytailアニメーションをD&Dします。今回は、Ponytailアニメーションを先にD&Dしています。
Animationパラメータの追加
Animatorウィンドウに先ほど作成したPigtailアニメーションとPonytailアニメーションをD&Dします。今回は、Ponytailアニメーションを先にD&Dしています。
 AnimatorレイヤーにアニメーションをD&D
「Any State」を右クリックしてコンテキストメニューから「Make Transition」をクリックし、出てきた矢印をPonytailとPigtailに接続してください。
AnimatorレイヤーにアニメーションをD&D
「Any State」を右クリックしてコンテキストメニューから「Make Transition」をクリックし、出てきた矢印をPonytailとPigtailに接続してください。
 Any StateとPigtail、PonytailをMake Transisionで接続
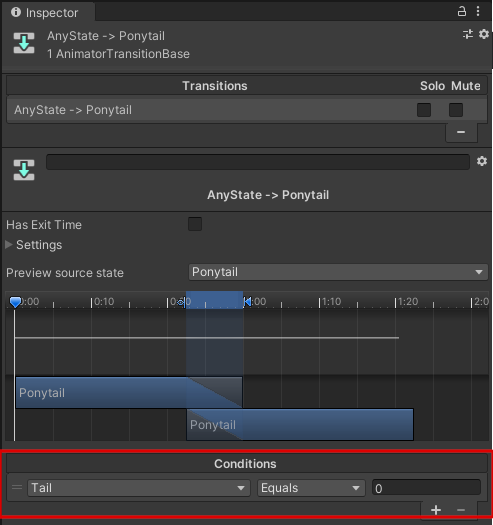
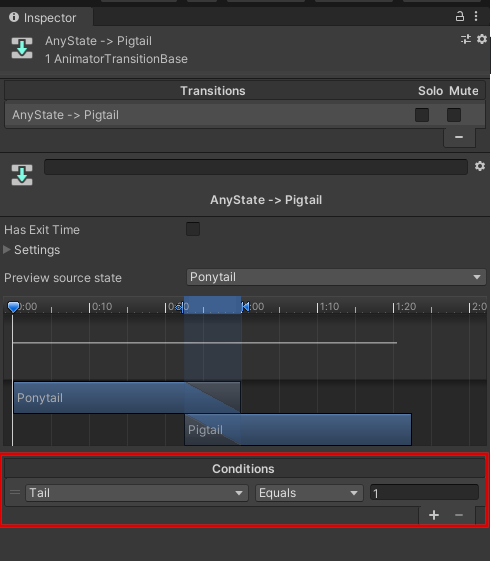
生成したTransition(矢印)をクリックし、Inspectorから以下の画像のように設定してください。
PonytailのTransitionの設定(右)とPigtailのTransitionの設定(左)
Any StateとPigtail、PonytailをMake Transisionで接続
生成したTransition(矢印)をクリックし、Inspectorから以下の画像のように設定してください。
PonytailのTransitionの設定(右)とPigtailのTransitionの設定(左)
以上でExpressionsの作成は終了です。
Avatar3.0 Emulatorというツールを使うと、ExpressionsをUnity上で試すことができます。ここでの使用方法の説明は省略しますが、いちいちVRChatにアップロードせずともExpressionsが確認できるため便利なので利用してみてください。
3.5. マテリアルの変更
現状だとnasuのシェーダーはUnityの標準のシェーダーになっており、本来の見た目になっていない(はず)です。そのためマテリアルを変えてあげます。
BodyとPigtail_tail_meshには「nasu_Pigtails_PC」を、Ponytail_tail_meshには「nasu_Ponytail_PC」をそれぞれD&Dで適用してください。これらのマテリアルは、Assets > Tigri_Nasu > Materialsにあります。
3.6. DynamicBoneの設定
※DynamicBoneを利用しない場合は、この項目は飛ばして良いです。
ピッグテールとポニーテールにDynamicBoneを設定します。
はじめに、nasu_Pigtail_PC(Prefab Asset)とnasu_Ponytail_PC(Prefab Asset)をHierarchyにD&Dします。
D&Dしたnasu_Pigtails_PC及びnasu_Ponytails_PCにはDynamic Boneのコンポーネントが付いていますので、それらをnasuにコピーしていきます。
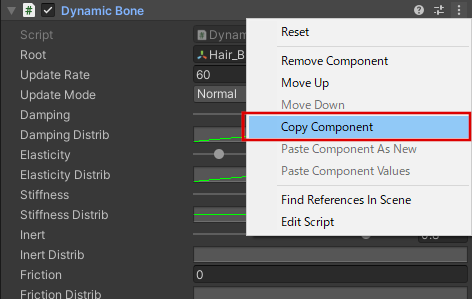
コンポーネントのコピーは、コンポーネントのタイトルを右クリック(もしくは、右端にある「…」を縦にしたようなマークをクリック)して、コンテキストメニューを開き「Copy Component」をクリックすることによってできます。
 コンポーネントのコピー
一方、コンポーネントのペーストは、ペースとしたいオブジェクトが持つコンポーネントの1つ(どれでも良い)のコンテキストメニューから、「Paste Component As New」をクリックすることによってできます。
コンポーネントのコピー
一方、コンポーネントのペーストは、ペースとしたいオブジェクトが持つコンポーネントの1つ(どれでも良い)のコンテキストメニューから、「Paste Component As New」をクリックすることによってできます。
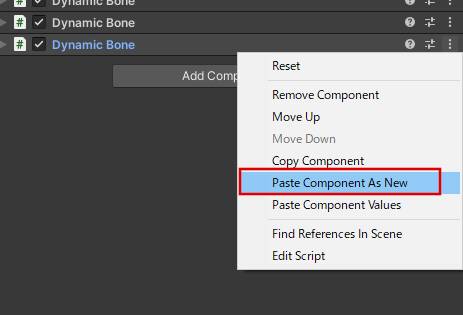 コンポーネントのペースト
ここでコピーするDynamic Boneのコンポーネントは4つです。
コンポーネントのペースト
ここでコピーするDynamic Boneのコンポーネントは4つです。
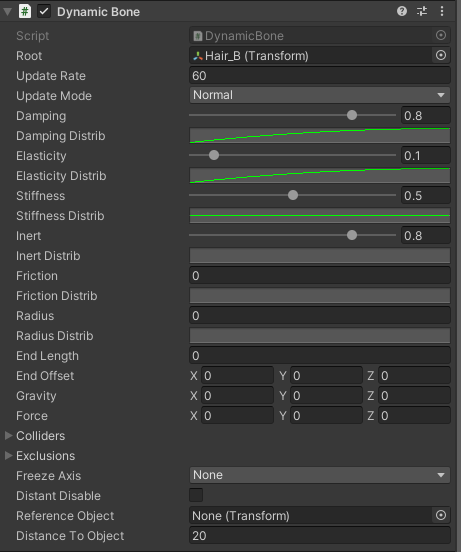
3つはnasu_Pigtails_PCが持つすべてのDynamic Boneコンポーネントで、最後の1つは、nasu_Ponytail_PCが持つ、「Root」に「Hair_B」が設定されているDynamic Boneコンポーネントです(以下の画像を参照)。
 nasu_Ponytail_PCからコピーするべきDynamic Boneコンポーネント
nasu_Ponytail_PCからコピーするべきDynamic Boneコンポーネント
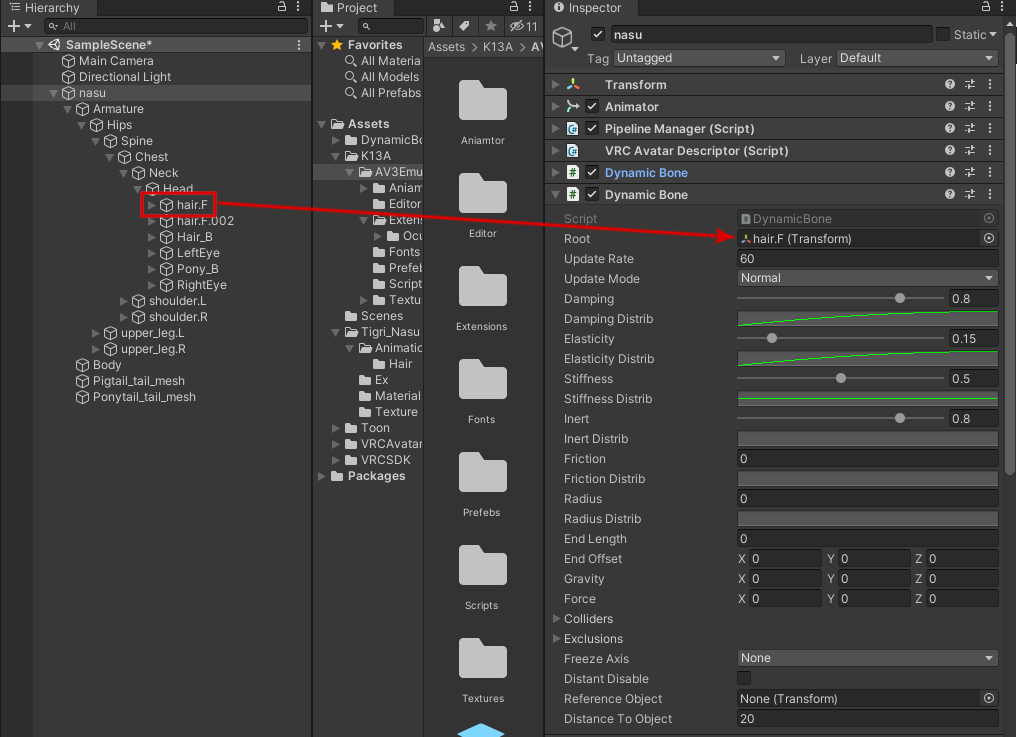
コピーしてきたこれらのDynamic Boneコンポーネントは、コピー元のボーンを参照しているため、ボーンの参照先を変える必要があります。Dynamic Boneが参照しているボーンはコンポーネント内の「Root」に設定されているボーンです。
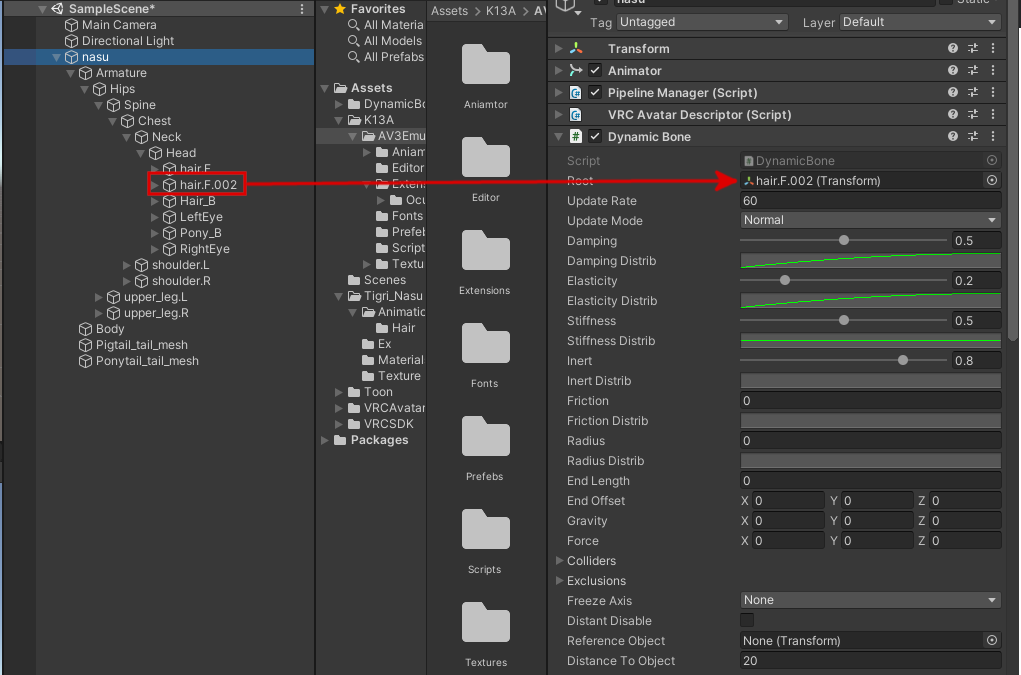
まずは、「hair.F」、「hair.F.002」を参照しているDynamic Boneは、nasuが持つ同名のボーンオブジェクトを参照させるようにします。
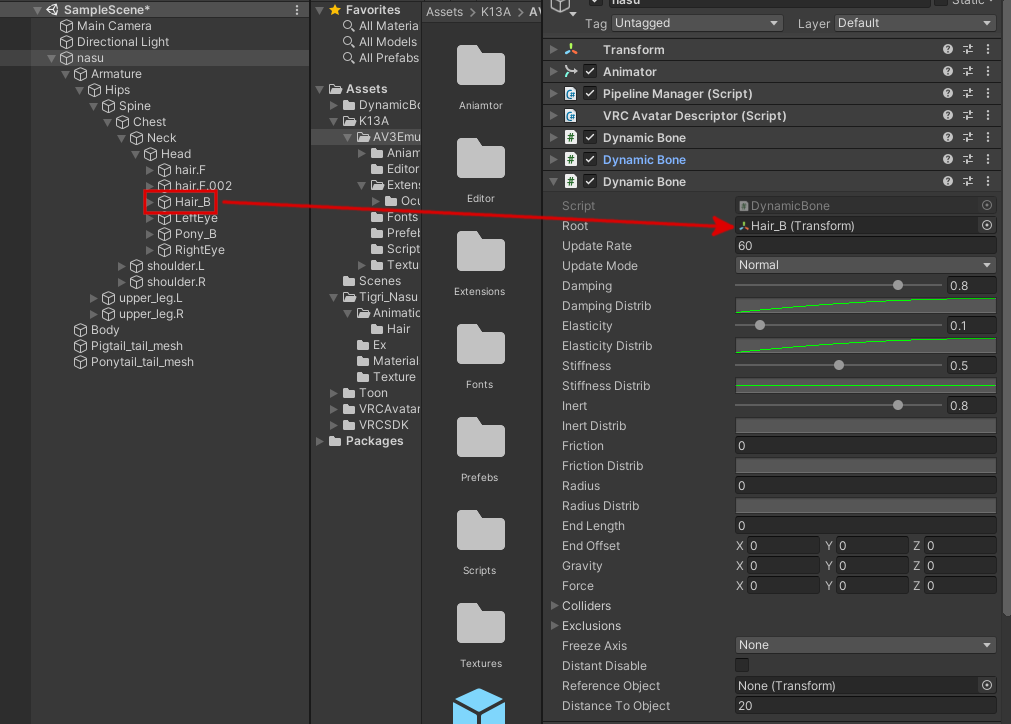
次に、nasu_Pigtails_PCからコピーしてきた「Hair_B」を参照しているDynamic Boneは、nasuの「Hair_B」を参照させるようにします。
最後に、nasu_Ponytails_PCからコピーしてきた「Hair_B」を参照しているDynamic Boneは、nasuの「Pony_B」を参照させるようにします。
nasuのDynamic Boneコンポーネント
シーンをプレイし、nasuを適当に左右に動かしてみてください。テールが揺れればDynamic Boneの設定は終了です。
3.7. VRChatにアップロードする
以上でアバターの基本的な設定は完了したので、アップロードしてください。
ここではアップロードについての説明は省略します。
Quest対応について
ここまでの説明はPC用アバターでの説明になります。
Quest用アバターで行いたい場合は、同様の手順をQuest用のなすちゃんに適用してください(QuestではDynamic Boneやユニティちゃんシェーダーが利用できないので、その手順は飛ばしてください)。
おわりに
なすちゃん改変の方法を備忘録的に記述しました。
見様見真似でやったのでもっと良い方法があると思っています(特にBlenderの分離と結合)。もし、もっと良い方法を知ってるという方はぜひ教えて下さい。
今回は単に髪型を切り替えるようにしただけですが、VRCのアバターは他にもたくさんのことができます。
VRCのアバター改変は楽しいので皆さんも色々改変してみましょう。
参照したページ